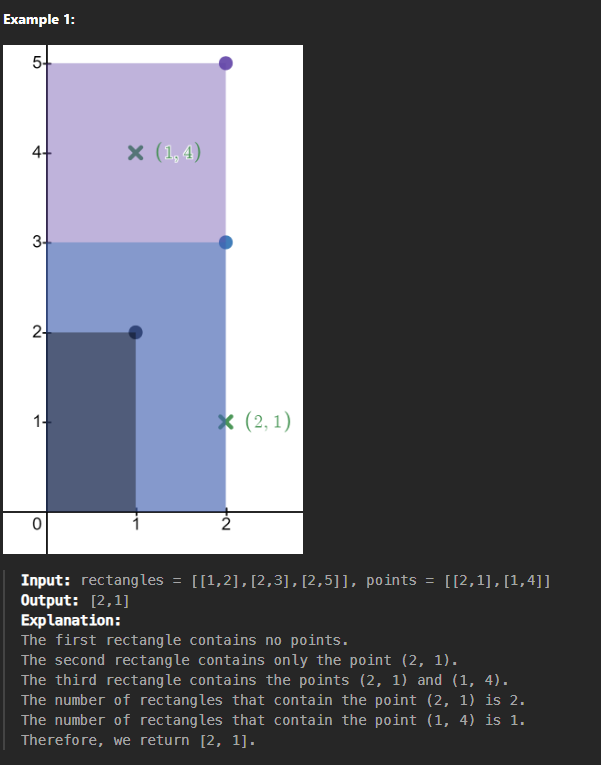
문제)
2차원 정수 배열 rectangles가 주어집니다.
여기서 rectangles[i] = [li, hi]는 i번째 직사각형의 길이가 li이고 높이가 hi임을 나타냅니다.
또한, 2차원 정수 배열 points가 주어지며, 여기서 points[j] = [xj, yj]는 좌표 (xj, yj)에 있는 점을 나타냅니다.
i번째 직사각형의 왼쪽 아래 모서리는 좌표 (0, 0)에 있고, 오른쪽 위 모서리는 좌표 (li, hi)에 있습니다.
배열 points의 각 점에 대해, 해당 점을 포함하는 직사각형의 개수를 반환하는 정수 배열 count를 구하십시오. 여기서 count[j]는 j번째 점을 포함하는 직사각형의 개수입니다.
i번째 직사각형이 j번째 점을 포함하는 경우는 다음 조건을 만족해야 합니다:
- 0≤yj≤hi
또한, 직사각형의 경계선 위에 있는 점도 포함된 것으로 간주됩니다.

문제 난이도 : 중
소요시간 및 풀이)
일단 문제를 보고 생각나는 대로 풀어보았다. 뭔가 너무 쉽게 풀리는거 같아서 불안했는데
역시나 시간 초과 발생.
너무 단순하게 접근한것 같아서 방법을 찾다가 정해놓은 시간이 다 돼서 정답을 확인했다.
정답 코드에서는 높이의 제한이 100인 것을 이용해서
모든 y좌표를 기준으로 직사각형들을 저장할 벡터 (hm)를 만들어 주고,
이 벡터에 직사각형의 좌표를 y값에 따라 저장해주었다.
그리고 이 벡터를 오름차순으로 정렬 후, 각 점에 대한 처리를 해주었다.
x좌표가 현재 점의 x좌표보다 크거나 같은 모든 직사각형을 확인하여 그 개수를 세려서 정답 벡터에 넣어주었다.
for 문에서 int i = y; 이므로 이미 직사각형의 y보다 크거나 같다.
소요 시간 : 못 품
오답 코드
class Solution
{
public:
vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points)
{
vector<int> vec;
for (auto point : points)
{
int count = 0;
for (int i = 0; i < rectangles.size(); i++)
{
if (rectangles[i][0] >= point[0] && rectangles[i][1] >= point[1])
{
count++;
}
}
vec.push_back(count);
}
return vec;
}
};
정답 코드
class Solution
{
public:
vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points)
{
// 모든 y좌표를 기준으로 직사각형들을 저장할 벡터
vector<vector<int>> hm(101);
//y 값에 따라 포인트를 저장합니다.
for (auto e : rectangles)
{
int x = e[0];
int y = e[1];
hm[y].push_back(x);
}
//binary search를 위해 오름차순 정렬
for (int i = 0; i < 101; i++)
{
sort(hm[i].begin(), hm[i].end());
}
vector<int> ans;
// 각 점에 대해 처리
for (auto e : points)
{
int x = e[0];
int y = e[1];
int cnt = 0;
//binary search를 사용하여 x 좌표가 현재 점의 x 좌표보다 크거나 같은 모든 직사각형을 확인
for (int i = y; i < 101; i++)
{
int idx = lower_bound(hm[i].begin(), hm[i].end(), x) - hm[i].begin();
cnt += (int)hm[i].size() - idx;
}
ans.push_back(cnt);
}
return ans;
}
};'코딩 테스트 연습' 카테고리의 다른 글
| LeetCode : 2284. Sender With Largest Word Count (0) | 2024.07.04 |
|---|---|
| 2320. Count Number of Ways to Place Houses (0) | 2024.07.03 |
| LeetCode : 650. 2 Keys Keyboard (0) | 2024.07.02 |
| LeetCode : 581. Shortest Unsorted Continuous Subarray (0) | 2024.07.02 |
| LeetCode : 384. Shuffle an Array (0) | 2024.07.02 |
