그리디 알고리즘

그리디 알고리즘은 개념은 굉장히 단순하다.

말 그대로 탐욕적으로, 눈 앞의 가장 큰 이익을 추구하는 기법이다.

실제 그리디 알고리즘을 검색하면 아래와 같이 나온다.

탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.

 

즉, 현재 상황에서 지금 당장 좋은 것 만 고르는 방법이다.
👉 매 순간 좋아 보이는 것만 선택
👉 현재의 선택이 나중에 미칠 영향에 대해 고려X

 

만약 다음과 같은 문제가 있다고 하자.

[문제]루트 노드부터 시작하여 거쳐가는 노드 값의 합을 최대로 만들어라.

 

그러면 정답은 아래 그림이 될 것이다.

 

 

하지만 그리디 알고리즘을 통해 문제를 풀면 아래와 같은 답이 나올 것이다.

 

 

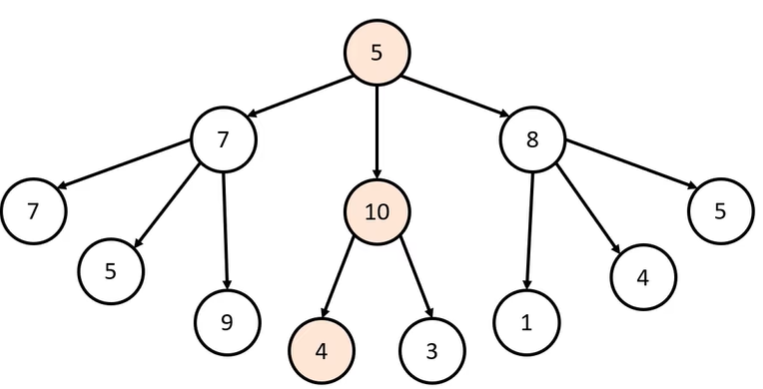
그리디 알고리즘은 이처럼 매 상황에서 가장 좋은 값을 찾아가는 방식이다.

 

이제 이 그리디 알고리즘을 사용한 간단한 문제를 풀어보자.

 

Q .  손님에게 거슬러야 할 돈이 N원일 때 거슬러 줘야 할 동전의 최소 개수?
(동전은 500원, 100원, 50원, 10원이 있다. )

#include <iostream>
using namespace std;

int n;//손님에게 받은 돈
int coin[4] = { 500, 100, 50, 10 };
int ans; //거스름돈의 개수
int main() {
    cin >> n;
    for (int i = 0; i < 4; i++) {
        ans += (n / coin[i]);
        n %= coin[i];
    }
    cout << ans;
}

 

위 코드가 그리디 알고리즘이 사용된 코드이다.

거슬러 줄 수 있는 가장 큰 화폐 단위부터 순서대로 사용해 나간다.

이 행동을 반목하면 문제를 풀어냈다.

 

이러한 방법으로 풀어낼 수 있는 이유는 작은 액수의 동전이 큰 액수 동전의 약수이기 때문이다.

즉, 100원 5개로 500원 한개를 만들 수 있다. 그렇기 때문에 큰 액수의 동전부터 사용해 나가면 최소 개수의 동전을 구할 수 있다.

---

정리를 해보자면 그리디 알고리즘은 특정 상황에서만 사용할 수 있다.

즉, 그리디를 사용한 방법이 정답이라는 보장이 되어야 사용할 수 있다.

위에서본 예제의 경우 동전간에 배수, 약수 관계가 성립했기 때문에 그리디를 사용할 수 있었다.

 

그래서 모두 그런것은 아니지만 그리디 문제는 일반적으로 최대한 적은, 최대한 많은 이라는 문구가 문제에 들어가는 경우가 많다. 최대/최소의 경우의 수를 구할것을 요구하는 문제들이다. 그리고 그리디를 사용할 수 있는 조건이 주어진다.

위 동전문제는 단순한 예시지만 동전간의 배수, 약수 관계가 그 조건이다. 물론 이러한 조건은 문제 내에 숨겨져있어 찾아내야 하는 경우가 많다.

 

그리디 알고리즘


1. 일반적으로 최대한 적은, 최대한 많은 이라는 문구가 문제에 들어가는 경우가 많다. 최대/최소의 경우의 수를 구할것을 요구하는 문제들이다.

2. 그리디를 사용할 수 있는 조건이 주어진다. (주로 문제를 읽고 조건을 찾아야한다.)

3.정렬을 한 뒤 그것을 이용해 푸는 문제가 많다. (위 동전문제의 경우에도 동전을 내림차순으로 정렬한 뒤 하나 하나 사용해 나가야 할 것이다.)